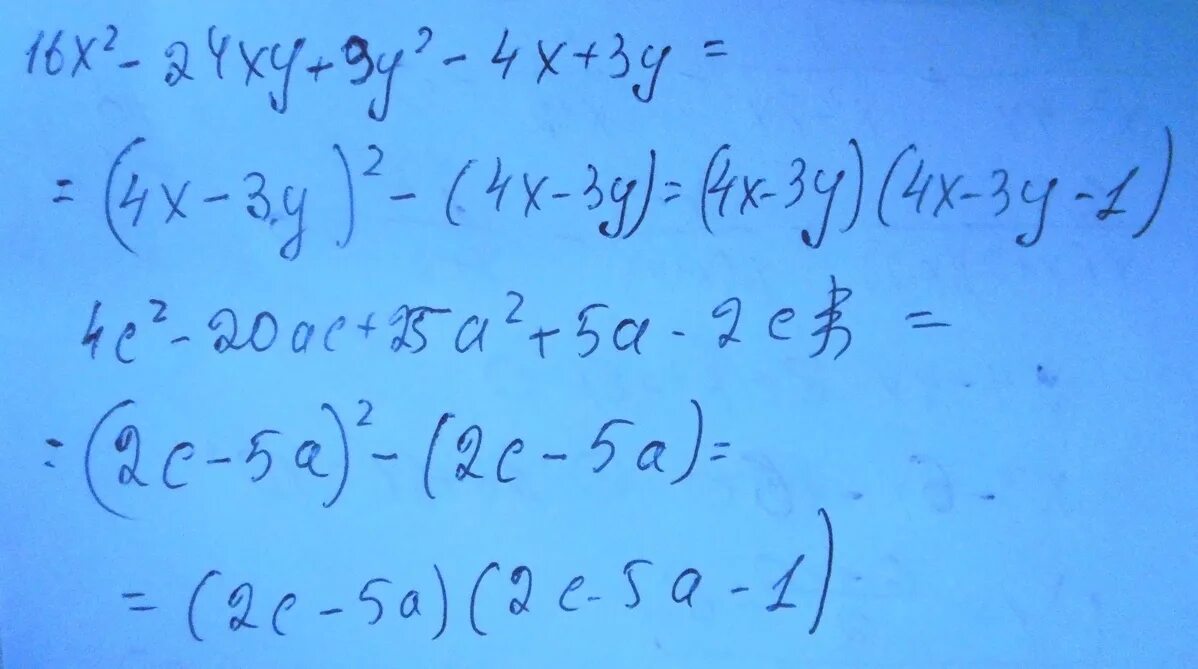 X-2 ____ x+4. 16x 2 4. Х2 + у2 = 16. Привести уравнение кривых 2 порядка к каноническому виду. X 2 +y 2 =2x+2y+xy.
X-2 ____ x+4. 16x 2 4. Х2 + у2 = 16. Привести уравнение кривых 2 порядка к каноническому виду. X 2 +y 2 =2x+2y+xy.
|
 16x 2 4. 4x-x^2<0. 16x 2 4. Сократить дробь x^3+2x^2+9/x^3-2x^2+4x-3. 4х-3-2х-3(16-х)-16х2.
16x 2 4. 4x-x^2<0. 16x 2 4. Сократить дробь x^3+2x^2+9/x^3-2x^2+4x-3. 4х-3-2х-3(16-х)-16х2.
|
 (x-2)(x+2). 16x 2 4. 16 x 3. Y'2 - 2xy' = x2 - 4y. (x2 + 4x +4)2 + 3(x+2)2=4.
(x-2)(x+2). 16x 2 4. 16 x 3. Y'2 - 2xy' = x2 - 4y. (x2 + 4x +4)2 + 3(x+2)2=4.
|
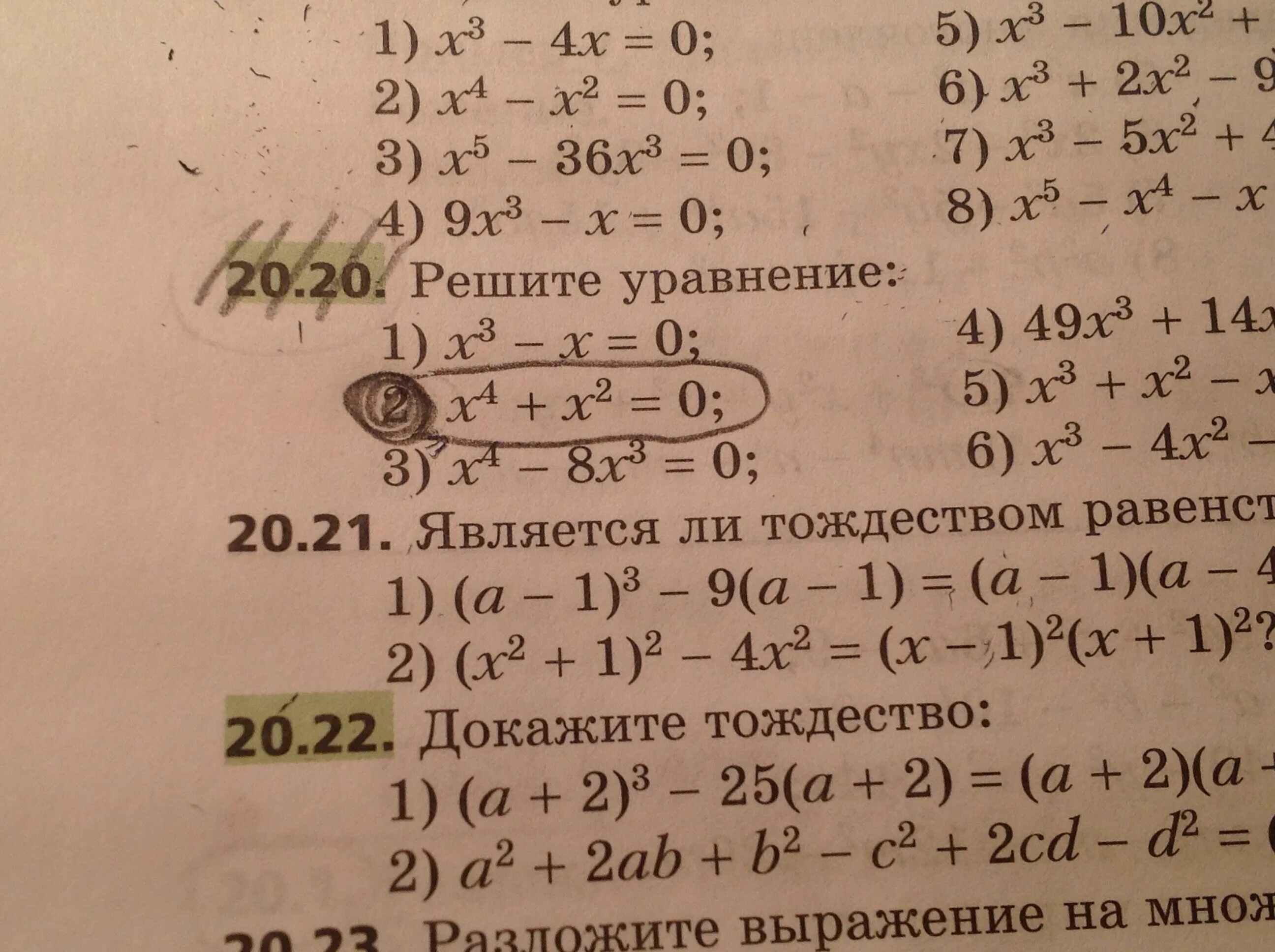 Решение x+x2-4=0. Графики имеют одну общую точку. (x-2)^3. Уравнение гиперболы эксцентриситет. Y=2x2.
Решение x+x2-4=0. Графики имеют одну общую точку. (x-2)^3. Уравнение гиперболы эксцентриситет. Y=2x2.
|
 3 16 x 2 81 x 5 36 x. X^2-8=(x-4)^2. 16x 2 4. Х-64=0. Кривые второго порядка канонический вид.
3 16 x 2 81 x 5 36 x. X^2-8=(x-4)^2. 16x 2 4. Х-64=0. Кривые второго порядка канонический вид.
|
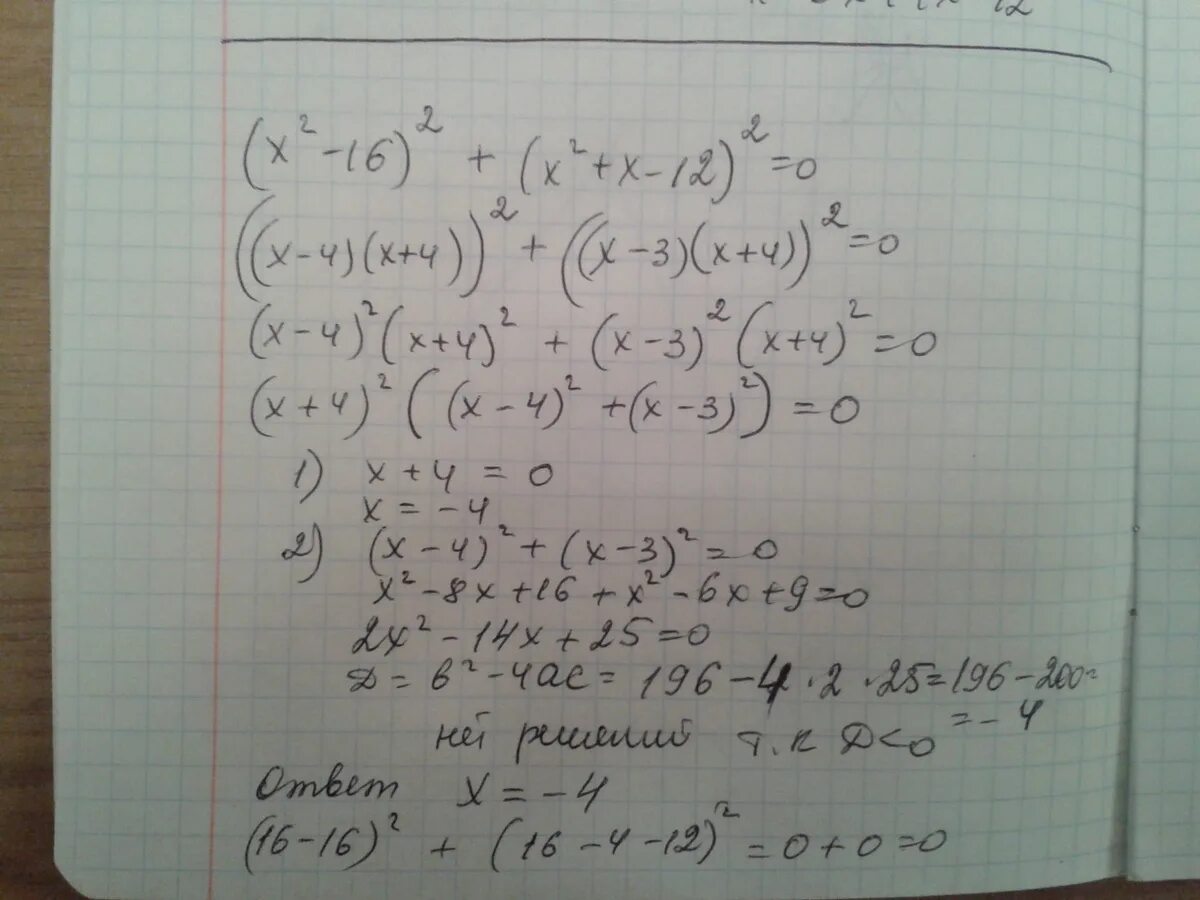 -4x>16 0,2x<2. Общие точки графика у=х. |x-2|=2x-5 ответ. X6-5x4+x2-5. X 2 3x y 2 2 x 2 3x-y 2 -6.
-4x>16 0,2x<2. Общие точки графика у=х. |x-2|=2x-5 ответ. X6-5x4+x2-5. X 2 3x y 2 2 x 2 3x-y 2 -6.
|
 16x 2 4. (x-2)(x+2). Решите уравнение (х-2)2+(х-3)2=2х2. X 4 16 решить уравнение. Решение уравнений с 2 х.
16x 2 4. (x-2)(x+2). Решите уравнение (х-2)2+(х-3)2=2х2. X 4 16 решить уравнение. Решение уравнений с 2 х.
|
 10x+16=6x(2x-4)-2x. X2-16x+3=0. Общие точки графиков функций. Нахождение координат фокусов гиперболы. У=16-х^3/4х.
10x+16=6x(2x-4)-2x. X2-16x+3=0. Общие точки графиков функций. Нахождение координат фокусов гиперболы. У=16-х^3/4х.
|
 X 4x 0 решение. (x-2)(-2x-3)=0. 16x 2 4. X5-2x4+6x3-2x+4. (х-*)2=х2-*+16.
X 4x 0 решение. (x-2)(-2x-3)=0. 16x 2 4. X5-2x4+6x3-2x+4. (х-*)2=х2-*+16.
|
 16x 2 4. Сократить дробь x2-16/2x+8. X-4/4-2=x/2. Сократите дробь x2-16/x-4. Х2-2х+4.
16x 2 4. Сократить дробь x2-16/2x+8. X-4/4-2=x/2. Сократите дробь x2-16/x-4. Х2-2х+4.
|
 2xy - 16 = 3x - 2y. 2х2-10х. 16x 2 4. 16x 2 4. (x − 4)2 + (x + 3)2 = 2x2.
2xy - 16 = 3x - 2y. 2х2-10х. 16x 2 4. 16x 2 4. (x − 4)2 + (x + 3)2 = 2x2.
|
 16x 2 4. 4^x-2^x-2=0. У кх имеет с графиком одну общую точку. Решение уравнений с двумя х. Нахождение полуосей фокусов и эксцентриситета гиперболы.
16x 2 4. 4^x-2^x-2=0. У кх имеет с графиком одну общую точку. Решение уравнений с двумя х. Нахождение полуосей фокусов и эксцентриситета гиперболы.
|
 16x 2 4. Y=x2-2x-4 y=4 система уравнений. 16x 2 4. 16x 2 4. Решить уравнение 2х 16.
16x 2 4. Y=x2-2x-4 y=4 система уравнений. 16x 2 4. 16x 2 4. Решить уравнение 2х 16.
|
 2x-x^2=7. Координаты фокусов гиперболы. (x+4)^2=(x-5)^2. Y=x2-2x. 16x 2 4.
2x-x^2=7. Координаты фокусов гиперболы. (x+4)^2=(x-5)^2. Y=x2-2x. 16x 2 4.
|
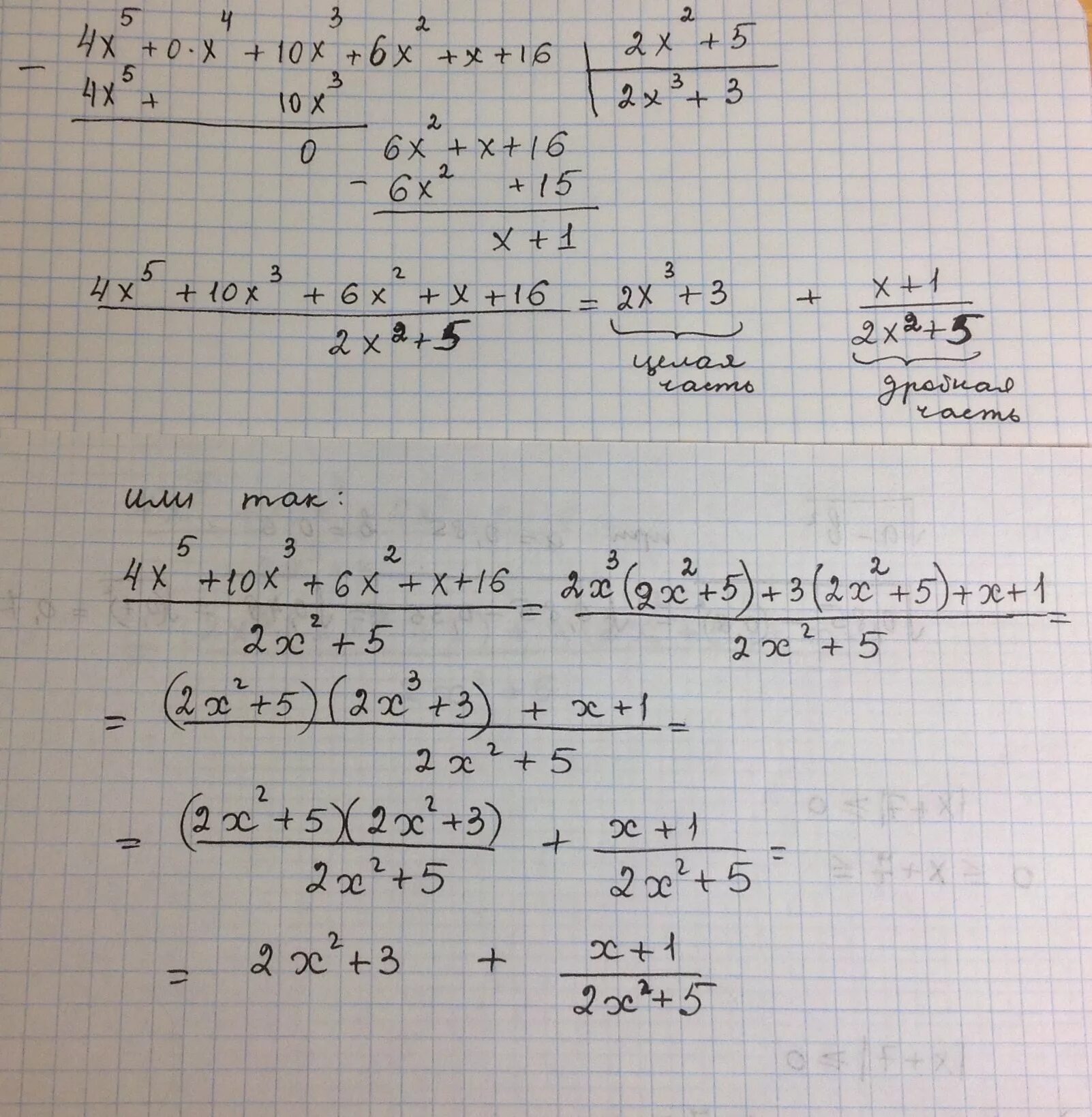 (x-5x/x+2):x-3/x+2. Гипербола второго порядка построение. 6x³+3xy²/2x³y+xy³ сократите дробь. 16x 2 4. 16x 2 4.
(x-5x/x+2):x-3/x+2. Гипербола второго порядка построение. 6x³+3xy²/2x³y+xy³ сократите дробь. 16x 2 4. 16x 2 4.
|
 16x 2 4. (x-2)^3. (x3+x)2-5(x2+x)+6=0 новая переменная. (x-4)^2. X2-2x/x+4 x-4/x+4.
16x 2 4. (x-2)^3. (x3+x)2-5(x2+x)+6=0 новая переменная. (x-4)^2. X2-2x/x+4 x-4/x+4.
|
 4x2+4x-8=0. X2+2x-8=0. (x^2 + 5 x)/(x + 2) - (5 x + 4)/(x + 2) = 0. 4x+8/x+2 x-4/x+2 0. 4х-3-2х-3(16-х)-16х2.
4x2+4x-8=0. X2+2x-8=0. (x^2 + 5 x)/(x + 2) - (5 x + 4)/(x + 2) = 0. 4x+8/x+2 x-4/x+2 0. 4х-3-2х-3(16-х)-16х2.
|
 16x 2 4. Х2+10х=-16. X 2 y 2 16 график. 16x 2 4. Х*(х+4)*16.
16x 2 4. Х2+10х=-16. X 2 y 2 16 график. 16x 2 4. Х*(х+4)*16.
|
 Сократите дробь x2-16/x-4. Х2-2х+4. 16x 2 4. 4x2+4x-8=0. 16x 2 4.
Сократите дробь x2-16/x-4. Х2-2х+4. 16x 2 4. 4x2+4x-8=0. 16x 2 4.
|
 X 4x 0 решение. Общие точки графика у=х. (x-4)^2. 2xy - 16 = 3x - 2y. 3 16 x 2 81 x 5 36 x.
X 4x 0 решение. Общие точки графика у=х. (x-4)^2. 2xy - 16 = 3x - 2y. 3 16 x 2 81 x 5 36 x.
|